HDLBits 포스팅은 Ligth Theme을 권장합니다.
(왼쪽 메뉴 하단)
문제는 반드시 HDLBits를 참고하세요! 보다 자세하게 적혀있습니다.
https://hdlbits.01xz.net/wiki/Hadd
Hadd - HDLBits
hdlbits.01xz.net
Arithmetic Circuits
Half Adder
Create a half adder. A half adder adds two bits (with no carry-in) and produces a sum and carry-out.
반가산기를 생성하세요. 반가산기는 (Carry-in 없이) 2-bit를 더하고 합계와 Carry-out을 생성합니다.
Solution ↓
module top_module(
input a, b,
output cout, sum );
assign cout = a & b;
assign sum = a ^ b;
endmodule
Full Adder
Create a full adder. A full adder adds three bits (including carry-in) and produces a sum and carry-out.
전가산기를 생성하세요. 전가산기는 3bit(carry-in 포함)를 더하고 합계와 carry-out을 생성합니다.
Solution ↓
module top_module(
input a, b, cin,
output cout, sum );
assign cout = (a & b) | (a & cin) | (b & cin);
assign sum = (a ^ b) ^ cin;
endmodule
3-bit Binary Adder
Make 3 instances of it to create a 3-bit binary ripple-carry adder. The adder adds two 3-bit numbers and a carry-in to produce a 3-bit sum and carry out.
3-bit 2진 ripple-carry 가산기를 만들기 위해 3가지 인스턴스를 만듭니다. 가산기는 3bit 숫자 2개와 carry-in을 더해서 3-bit 합을 만들어 수행합니다.
Solution ↓
module top_module(
input a, b, cin,
output cout, sum );
assign cout = (a & b) | (a & cin) | (b & cin);
assign sum = (a ^ b) ^ cin;
endmodule
Adder
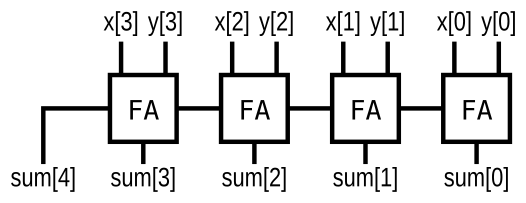
Implement the following circuit:
다음 회로를 구현하세요.
Solution ↓
module top_module (
input [3:0] x,
input [3:0] y,
output [4:0] sum);
reg carry0, carry1, carry2;
assign sum[0] = x[0] ^ y[0];
assign carry0 = x[0] & y[0];
assign sum[1] = x[1] ^ y[1] ^ carry0;
assign carry1 = (x[1] & y[1]) | (x[1] & carry0) | (y[1] & carry0);
assign sum[2] = x[2] ^ y[2] ^ carry1;
assign carry2 = (x[2] & y[2]) | (x[2] & carry1) | (y[2] & carry1);
assign sum[3] = x[3] ^ y[3] ^ carry2;
assign sum[4] = (x[3] & y[3]) | (x[3] & carry2) | (y[3] & carry2);
endmodule
Signed Addition Overflow
Assume that you have two 8-bit 2's complement numbers, a[7:0] and b[7:0]. These numbers are added to produce s[7:0]. Also compute whether a (signed) overflow has occurred.
a[7:0]과 b[7:0]의 8-bit 2의 보수를 두 개 가지고 있다고 가정합시다. 이 숫자들은 s[7:0]을 생성하기 위해 더해집니다. 또한 (signed) 오버플로우가 발생했는지 여부도 계산해야 합니다.
Solution ↓
module top_module (
input [7:0] a,
input [7:0] b,
output [7:0] s,
output overflow
);
assign s = a + b;
assign overflow = ((a[7] == b[7]) && (s[7] != a[7]));
endmoduleoverflow 조건
1. a, b가 양수이지만, 결과가 음수일 때
2. a, b가 음수이지만, 결과가 양수일 때
overflow를 통해 a, b의 부호를 확인하고, 계산 결과와의 부호가 일치하는 지를 확인하여 Overflow를 결정한다.
100-bit Binary Adder
Create a 100-bit binary adder. The adder adds two 100-bit numbers and a carry-in to produce a 100-bit sum and carry out.
100-bit 이진 가산기를 만드세요. 가산기는 100-bit 숫자 두 개와 carry-in을 더해서 100-bit 합을 만들고 수행합니다.
Solution ↓
module top_module(
input [99:0] a, b,
input cin,
output cout,
output [99:0] sum );
assign {cout, sum} = cin + a + b;
endmodule
4-digit BCD Adder
You are provided with a BCD (binary-coded decimal) one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out.

Instantiate 4 copies of bcd_fadd to create a 4-digit BCD ripple-carry adder. Your adder should add two 4-digit BCD numbers (packed into 16-bit vectors) and a carry-in to produce a 4-digit sum and carry out.
BCD 숫자 2개와 carry-in을 추가하고 합계와 carry-out을 생성하는 BCD(이진 부호 십진법) 1자리 덧셈기 bcd_fadd가 제공됩니다.
4자리 BCD 리플 캐리어 가산기를 만들려면 bcd_fad의 복사본 4개를 인스턴스화합니다. 가산기는 4자리 BCD 숫자 2개(16-bit 벡터로 포장)와 carry-in을 추가하여 4자리 합을 생성하고 수행해야 합니다.
Solution ↓
module top_module (
input [15:0] a, b,
input cin,
output cout,
output [15:0] sum );
wire [3:0] carry_out;
bcd_fadd uut0(
.a (a[3:0]),
.b (b[3:0]),
.cin(cin),
.cout(carry_out[0]),
.sum(sum[3:0])
);
bcd_fadd uut1(
.a (a[7:4]),
.b (b[7:4]),
.cin(carry_out[0]),
.cout(carry_out[1]),
.sum(sum[7:4])
);
bcd_fadd uut2(
.a (a[11:8]),
.b (b[11:8]),
.cin(carry_out[1]),
.cout(carry_out[2]),
.sum(sum[11:8])
);
bcd_fadd uut3(
.a (a[15:12]),
.b (b[15:12]),
.cin(carry_out[2]),
.cout(carry_out[3]),
.sum(sum[15:12])
);
assign cout = carry_out[3];
endmodule
'Circuit Design > 🚀HDLBits' 카테고리의 다른 글
| [HDLBits] 9. Circuit - Combinational Logic (4) (0) | 2024.08.29 |
|---|---|
| [HDLBits] 7. Circuit - Combinational Logic (2) (1) | 2024.07.14 |
| [HDLBits] 6. Circuits - Combinational Logic(1) (0) | 2024.07.11 |
| [HDLBits] 5. Verilog Language - More Verilog Features (0) | 2024.07.11 |
| [HDLBits] 4. Verilog Language - Procedures (0) | 2024.07.08 |
