A General Lower Bound for Sorting
이 섹션에서는 비교 기반 정렬 알고리즘은 아무리 잘 만들어도 최악의 경우 O(N log N)은 피할 수 없다는 사실을 이론적으로 증명합니다. 즉 mergesort나 quicksort처럼 O(N log N) 정렬은 이미 최적에 가깝다는 걸 수학적으로 보여주는 파트입니다.
Decision Trees :
최소 복잡도 (Lower Bound)를 증명하는 데 사용되는 추상 개념
비교 기반 정렬은 결국 비교 연산으로만 결정되고, 이 과정을 이진 트리 결정(decision tree)으로 표현할 수 있습니다.

위 사진의 트리는 비교 기반 정렬 알고리즘이 어떤 순서로 원소를 비교할 지에 따라 순열 중 하나를 선택하게 되는 과정을 모델링한 것입니다. 루트에서 시작해서, 비교 결과에 따라 왼쪽/오른쪽 자식 노드로 내려가고, 리프 원소에 도달했을 때, a, b, c의 정렬 순서가 확정됩니다.
- 루트 노드에선 가능한 6가지 순열이 있습니다. 첫 비교는 a < b 결과에 따라 서브트리로 진행합니다.
- 왼쪽 서브트리 a < b 다음 비교 a < c, c < a
... - 오른쪽 서브트리 b < a 다음 비교 b < c, c < b
...
최종 리프 노드는 6개(8, 9, 5, 10, 11, 7) 가 나옵니다
3개에 요소에 대해서 6개의 순열이 나왔습니다. 이걸 식으로 표현해 보면
(세 개 요소 → 6개 순열 → 최소 log₂(6) ≈ 2.58 → 최소 3번 비교 필요)

깊이 d인 이진 트리는 최대 2^d개의 리프 노드를 가질 수 있다.(깊이가 커질 수록 리프 노드 수는 늘어날 수 있다.)

리프 노드가 L개 있는 이진 트리는 깊이가 최소 log₂L 이상이어야 한다.

비교만 사용하는 정렬 알고리즘은 최악의 경우 최소 log₂(N!) 번의 비교가 필요하다.

정렬 알고리즘은 평균적으로도 Ω(N log N) 번의 비교가 필요하다.
- 정렬하려는 입력이 N개일 때 가능한 모든 순열은 N! 개.
- 각 순열은 decision tree의 하나의 리프 노드에 해당.
- 트리의 깊이는 곧 비교 횟수의 최악 케이스를 의미.
- 따라서, 정렬 알고리즘이 최소한 구해야 하는 비교 횟수는 log(N!) 이상.
Decision-Tree Lower Bounds for Selection Problems
정렬이 아니라, k번째로 작은 원소를 찾는 문제 (중간값, 최솟값처럼)를 다룰 때도, 비교 기반 알고리즘은 특정 개수 이상의 비교가 반드시 필요하다는 걸 증명하고 있습니다.

1. 최솟값 찾기 : N개의 원소 중 최솟값을 찾으려면, 최소 N-1번의 비교가 필요합니다. 왜냐하면 각 원소가 한 번 이상 다른 원소에게 지지 않으면 최솟값일 수 없기 때문입니다.
2. 최댓값도 마찬가지로 N-1 번의 비교가 필요하고
3. 중간값 찾기 : N개 중 정확히 N/2 번째로 작은 값을 찾는 건, 단순히 정렬 후 N/2번째 원소를 보는 것보다 더 나은 방법이 있을까. 하지만 이론적으로, Ω(N) 이상 걸리고, 최악의 경우 Ω(N log N)까지 가능합니다.

어떤 비교 기반 알고리즘도 N개의 원소에서 최솟값을 찾으려면 N-1번 비교해야 한다.

N개 중 k번째로 작은 원소를 찾기 위한 결정 트리는 최소
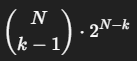
개의 리프 트리를 가져야 한다.

k번째로 작은 원소를 찾으려면 최소한

번의 비교가 필요하다.

두 번째로 작은 원소를 찾으려면 최소

번 비교해야 한다.

비교 기반 알고리즘은 중간값을 찾기 위해 최소

번 비교해야 한다.
Adversary Lower Bounds(적대자 하한 분석)
Adversary Model은 정렬/선택 알고리즘이 어떤 비교를 하든 간에, 최악의 상황을 가정하여 하한(bound)을 분석하는 기법입니다.
기존의 결정 트리 기반의 하한은 느슨하고 현실적인 하한이 아닙니다. 최솟값 찾기는 결정 트리 방식으로 log N이지만, 실제로는 N-1번 비교가 필요하고,
이걸 adversary argument로 보강했으며, 이를 확장해서 최솟값과 최댓값 동시 찾기에도 적용합니다.
예를 들어, N = 6일 때 min과 max를 동시에 찾으려면, 3쌍을 비교해서 각 쌍의 이긴 쪽은 max 후보, 진 쪽은 min 후보로 나눠서 각각 N/2 - 1번 추가 비교합니다. 결론적으로, 총 3N/2 -2 번은 필요한 더 타이트한 하한이 존재하는 것을 알 수 있습니다.
이러한 Adversary 모델은 알고리즘 구조에 관계없이 필요한 최소 비교 수를 도출해 주는 기법입니다.
total information(정보 단위)과 comparison(비교)의 개념이 있는데, 몇 번의 비교로 몇 개의 단위 정보를 얻을 것인가? 에 대한 질문에서 Adversary Lower Bound는 적은 비교로 많은 단위 정보를 획득할 수 있는 비교의 하한이 얼마인가를 다룹니다. 여기서 정보 단위는 고정된 값이고, comparison은 그 정보를 얼마나 효율적으로 얻는가에 대한 개수입니다. comparison을 줄인다면 적은 연산이 가능할 테니, 어떻게 하면 comparison을 줄일 수 있나에 대한 물음읍니다.

교재에서는 N = 6인 상황을 예로 들며 설명하고 있다.
N = 6이라면, naive하게 MIN, MAX 모두 보는 상황에서는 2N - 2가 나옵니다.
그러면 여기서 total information = 10, comparison(naive) = 10이 된다고 합시다.
하지만 Adversary로 해보면 comparison을 더 줄일 수 있다는 겁니다.
6개를 3쌍으로 묶어서 두 개씩 비교하면 각각 W/L를 확인할 수 있을 것입니다. 여기서 총 10의 total information 중 6을 사용합니다(2 * N/2). 그러면 남은 total information은 4.
나머지는 기본 비교 연산으로 한다고 가정하면, 처음 N/2의 연산에 사용한 비교 횟수(3) + 나머지 4회 기본 연산으로
3 + 4 = 7으로 기존 naive 방식보다 비교 횟수를 줄일 수 있습니다.
Linear-Time Sorts
비교 기반 정렬은 아무리 잘해도 Ω(N log N) 하한이 있다고 말해왔습니다. 하지만 특정 조건(숫자 범위, 구조) 등이 갖춰지면, 비교 없이도 O(N)에 정렬이 가능합니다. 대표적으로 Bucket Sort, Radix Sort가 있습니다.
Bucket Sort
정렬할 값들을 여러 버킷에 나눠 담습니다.
각 버킷 안에 값들은 보통 insertion sort 같은 간단한 방식으로 정렬합니다.
마지막으로 버킷들을 순서대로 이어 붙이면 정렬이 완료됩니다.
조건 : 입력 데이터가 0~1 사이 실수값처럼 균등하게 분포되어 있을 때 아주 빠릅니다.
입력 배열 A [1... N]은 0 이상 M 미만의 양의 정수만을 포함해야 한다. (= 값의 범위가 작을 때만 유효)
// 배열 A가 0 이상 M 미만의 정수로 구성되어 있다고 가정
int count[M] = {0}; // M 크기의 카운트 배열, 전부 0으로 초기화
// 1단계: 각 숫자에 대한 카운트
for(int i = 0; i < N; ++i)
++count[A[i]];
// 2단계: count 배열을 스캔하며 정렬된 결과를 출력
for(int i = 0; i < M; ++i)
for(int j = 0; j < count[i]; ++j)
print i;
입력
A = [2, 3, 3, 1, 0, 2], M = 4count = [1, 1, 2, 2]
출력
0 1 2 2 3 3
Radix Sort
자릿수(digit)를 기준으로 정렬합니다. (가장 낮은 자릿수부터)
각 자릿수에 대해 Counting Sort 같은 안정 정렬을 수행합니다.
정수 또는 고정 자릿수 문자열 정렬에 적합합니다.
조건 : 비교가 아니라 문자의 위치나 숫자의 자릿수로 판단 가능할 때 사용
Radix Sort
/*
* Radix sort an array of Strings
* Assume all are all ASCII
* Assume all have same length
*/
void radixSortA( vector<string> & arr, int stringLen )
{
const int BUCKETS = 256;
vector<vector<string>> buckets( BUCKETS );
for( int pos = stringLen - 1; pos >= 0; --pos ) // 뒤에서부터 시작
{
for( string & s : arr )
buckets[ s[ pos ] ].push_back( std::move( s ) );
int idx = 0;
for( auto & thisBucket : buckets )
{
for( string & s : thisBucket )
arr[ idx++ ] = std::move( s );
thisBucket.clear( ); // 다음 자릿수를 위한 초기화
}
}
}BUCKETS = 256 : ASCII 문자 전체를 위한 256개의 버킷.
stringLen : 모든 문자열의 길이는 같다고 가정.
문자열의 끝 문자부터 시작해서 앞 문자로 이동하면서 정렬.
- LSD부터 정렬해야 이전 단계에서 결정된 순서를 유지할 수 있기 때문 (stable sort가 필요).
예를 들어 다음과 같은 문자열 배열이 있다고 하면,
[ "cab", "dad", "bee", "bad", "ace" ]정렬 순서는
- 3번째 문자 (pos=2) 기준 버킷 정렬
- 2번째 문자 (pos=1) 기준 버킷 정렬
- 1번째 문자 (pos=0) 기준 버킷 정렬
이 과정을 거치면 최종적으로 사전 순 정렬이 된다.
Counting Radix Sort
/*
* Counting radix sort an array of Strings
* Assume all are ASCII
* Assume all have same length
*/
void countingRadixSort( vector<string> & arr, int stringLen )
{
const int BUCKETS = 256; // ASCII 문자는 256개
int N = arr.size( );
vector<string> buffer( N ); // 결과 저장용 버퍼
vector<string> *in = &arr; // 현재 정렬할 배열
vector<string> *out = &buffer; // 결과 저장 배열
for( int pos = stringLen - 1; pos >= 0; --pos ) // 문자 맨 뒤에서 앞으로
{
vector<int> count( BUCKETS + 1 ); // 개수 세기용 배열
// 1단계: 각 문자의 개수 세기
for( int i = 0; i < N; ++i )
++count[ (*in)[ i ][ pos ] + 1 ];
// 2단계: 누적합 구해서 정렬 위치 계산
for( int b = 1; b <= BUCKETS; ++b )
count[ b ] += count[ b - 1 ];
// 3단계: 실제 문자열을 out 배열에 정렬하여 복사
for( int i = 0; i < N; ++i )
(*out)[ count[ (*in)[ i ][ pos ] ]++ ] = std::move( (*in)[ i ] );
// 4단계: 포인터 스왑 - 다음 루프를 위해 in/out 교체
std::swap( in, out );
}
// 정렬 횟수가 홀수면 buffer에 최종 결과가 있음 -> arr로 복사
if( stringLen % 2 == 1 )
for( int i = 0; i < arr.size( ); ++i )
(*out)[ i ] = std::move( (*in)[ i ] );
}위 알고리즘은 Radix Sort의 일종으로, 각 자릿수를 오른쪽에서 왼쪽으로 보면서 정렬합니다.
버킷을 실제 리스트(vector<vector>)로 저장하는 대신, count 배열을 사용해서 자리를 계산합니다. 이게 Counting Radix Sort의 핵심 최적화입니다.
각 pass는 안정 정렬(stable sort)을 보장하며, 이전 자릿수의 정렬 순서가 보존됩니다.
입력 문자열의 길이가 L이고 N개의 문자열이 있을 때, 전체 time complexity는 O(L x N).
Radix Sort for Variable-Length Strings
void radixSort(vector<string>& arr, int maxLen)
{
const int BUCKETS = 256; // ASCII 문자 수 (0 ~ 255)
// Step 1: 문자열 길이에 따라 분류
vector<vector<string>> wordsByLength(maxLen + 1);
vector<vector<string>> buckets(BUCKETS); // 정렬용 버킷
for (string& s : arr)
wordsByLength[s.length()].push_back(std::move(s)); // 길이별로 저장
// Step 2: 짧은 문자열부터 arr에 재배치
int idx = 0;
for (auto& wordList : wordsByLength)
for (string& s : wordList)
arr[idx++] = std::move(s); // 길이 순 정렬
// Step 3: 뒤에서부터 자릿수별로 정렬 수행
int startingIndex = arr.size(); // 정렬 대상 시작 위치
for (int pos = maxLen - 1; pos >= 0; --pos)
{
startingIndex -= wordsByLength[pos + 1].size(); // 현재 길이의 시작 인덱스
// 해당 자릿수(pos)를 기준으로 문자 버킷에 분배
for (int i = startingIndex; i < arr.size(); ++i)
buckets[arr[i][pos]].push_back(std::move(arr[i]));
// 버킷에서 다시 arr에 복사 (정렬된 순서로)
idx = startingIndex;
for (auto& thisBucket : buckets)
{
for (string& s : thisBucket)
arr[idx++] = std::move(s);
thisBucket.clear(); // 다음 라운드를 위해 비움
}
}
}
1. 전처리 : 문자열을 길이별로 버킷에 나눕니다.
for( string & s : arr )
wordsByLength[ s.length() ].push_back( std::move( s ) );→ 문자열을 길이에 따라 분류하고, 길이 별로 버킷 정렬을 수행합니다.
2. arr 배열 길이 순으로 다시 재배치
for( auto & wordList : wordsByLength )
for( string & s : wordList )
arr[ idx++ ] = std::move( s );→ 짧은 문자열부터 긴 문자열 순서대로 정렬된 arr.
3. Radix Sort 진행 (뒤에서부터 문자별 정렬)
for( int pos = maxLen - 1; pos >= 0; --pos )- 각 위치(pos)마다 해당 위치에 문자가 있는 문자열만 정렬 대상으로 합니다.
- 이 때 어떤 문자열이 포함되는지 계산하기 위해 startingIndex를 사용합니다.
4. 문자 버킷에 분배
for( int i = startingIndex; i < arr.size(); ++i )
buckets[ arr[i][pos] ].push_back( std::move( arr[i] ) );ASCII 기준으로 각 문자를 256개 버킷에 분배
5. arr에 다시 재배치
for( auto & thisBucket : buckets )
{
for( string & s : thisBucket )
arr[ idx++ ] = std::move( s );
thisBucket.clear();
}- 각 버킷을 순서대로 순회하며 arr 배열에 재배치
정리하자면,
- 버킷 정렬로 문자열을 길이 순으로 먼저 정렬하고,
- 문자열의 뒷 문자부터 앞 문자 순으로 문자 기준으로 정렬합니다.
- 길이 기반 초기 정렬은 버킷 정렬로 충분히 빠르게 수행가능하기 때문에
전체 문자열 수가 N이고 각 문자열 길이의 합이 M이면, 전제 time complexity는 O(M)입니다.
External Sorting
지금껏 다룬 정렬 알고리즘은 모두, 모든 데이터가 메모리에 존재한다고 가정하고 있습니다.
우리가 다루는 데이터가 메모리(RAM)에 전부 올라갈 수 있을 만큼 작다면, 일반적인 내부 정렬 알고리즘(예: 퀵소트, 힙소트)만으로도 충분히 빠르게 정렬이 가능합니다. 하지만 실제 현업에서는 수십 GB, 수백 GB에 달하는 데이터를 정렬해야 할 일이 많고, 이 경우에는 데이터를 디스크에 저장한 채로 정렬해야 하는 상황이 생기는데, 이때 사용하는 방식이 외부 정렬(external sorting)입니다.
디스크는 메모리보다 훨씬 느린 장치고, 특히 무작위로 데이터를 읽는 랜덤 접근(random access)이 매우 비효율적입니다. 예를 들어 디스크가 초당 100번 정도밖에 접근하지 못한다면,
1GB 데이터를 정렬하려고 해도, 각 레코드가 100바이트면 총 1,000만 개의 레코드가 있는 셈이고, 최소한 1,000만 번의 비교가 필요합니다. 이 비교마다 디스크 접근이 발생한다고 가정하면, 총 100,000초 = 약 28시간이 걸릴 수 있다는 계산이 나옵니다. 이처럼, 단순한 방식으로는 현실적으로 불가능에 가까운 시간 소모가 생기기에 이에 맞춘 새로운 알고리즘이 필요합니다.
이런 이유 때문에, 디스크를 효율적으로 다루기 위한 특수한 정렬 알고리즘이 필요합니다. 특히 디스크 중에서도 테이프 드라이브처럼 제약이 큰 장치를 대상으로 한 외부 정렬 알고리즘은 순차 접근만 가능하고, 랜덤 접근은 불가능하다는 점을 생각해야 합니다.
효율적인 외부 정렬을 하기 위해서는 최소한 3개의 테이프 드라이브가 필요합니다
그 중 2개는 실제 정렬(merge, split)에 사용되고,
나머지 하나는 작업 전환, 보조 역할을 하면서
정렬 흐름을 매끄럽게 만들어줍니다.
만약 테이프 드라이브가 1개뿐이라면,정렬 중간 결과를 다시 읽고 다시 쓰는 과정이 반복되어야 하므로 최악의 경우 Ω(N²)에 가까운 디스크 접근 횟수가 필요하게 됩니다.
Simple Algorithm
기본적인 외부정렬 알고리즘은 mergesort에서 사용하는 merge 알고리즘을 이용합니다.
Ta1, Ta2, Tb1, Tb2라는 네 개의 테이프가 있다고 해봅시다. 이 테이프들 중 어떤 테이프가 입력 역할을 하고, 어떤 테이프가 출력 역할을 할지는 단계에 따라 바뀝니다.

처음에는 모든 데이터가 Ta1에 저장되어 있고, 내부 메모리에는 한 번에 M개의 레코드를 올릴 수 있다고 가정합니다. 이때 가장 자연스러운 첫 단계는
- Ta1에서 M개의 메모리를 읽고, 내부 메모리에서 이를 정렬합니다.
- 그 후, 정렬된 데이터를 Tb1, Tb2에 번갈아 가며 저장합니다.

이렇게 만들어진 정렬된 조각을 런(run)이라고 부릅니다. 입력이 모두 처리될 때까지 이 과정을 반복하면, Tb1, Tb2에 여러 개의 런이 만들어집니다. 이제 본격적인 병합 단계에 들어갑니다.
- 먼저 Tb1, Tb2에서 첫 번째 런을 꺼내 병합한 뒤,
- 결과를 Ta1에 저장합니다. (이 병합 결과는 원래 런보다 2배 더 긴 런)

그 다음 런을 꺼내 병합하고, Ta2에 저장합니다. 이렇게 Tb1, Tb2에 남은 모든 런을 처리할 때까지 Ta1, Ta2에 번갈아 병합 결과를 저장합니다. 만약 한쪽 테이프에 마지막 런 하나만 남았다면, 그 런은 그대로 적절한 테이프에 복사합니다.

병합이 끝났으면, 네 개의 테이프를 모두 되감고, 이번엔 역할을 바꿔 Ta1, Ta2를 입력 테이프로 Tb1, Tb2를 출력 테이프로 사용합니다. 이렇게 하면 런의 길이는 총 4M으로 늘어납니다.

이 과정을 반복하여 마지막에 전체 데이터를 담은 하나의 긴 런이 생성되면 정렬이 완료됩니다.
Multiway Merge
먼저 알고가야 할 점. 앞에서 사용한 방법은 run을 두 개로 나눠서 계속 merge하는 방법이라 2-way merge라고들 부릅니다. 근데 run을 늘리면 값을 효율적으로 갖고 올 수있다고 해서 설명할 k-way merge가 있습니다. 사실 2k개가 필요하긴 한데, 그것보다 중요한 게 queue입니다.
queue는 FIFO 구조를 갖는 컨테이너입니다. 하지만 우리가 다루는 priority queue는 일반 queue와는 다르게 우선순위에 따라서 나가는 heap 자료 구조입니다.(근데 왜 queue 라는 이름이 붙었을까) Default는 가장 큰 값이 우선순위가 높지만, greater를 사용해서 가장 작은 값을 루트에 위치시킬 수 있습니다. 그 후 pop을 사용해서 뺄 수도 있고, deleteMin이나 exctractMin을 만들어서 구성하는 방법도 있습니다. (greater + pop 이 직관적이고 편합니다.)

외부 정렬에서 정렬 성능을 향상시키기 위해 사용할 수 있는 한 가지 방법은, merge 과정에서 더 많은 테이프를 활용하는 것입니다. 기존의 기본 알고리즘에서는 두 개의 런을 병합하는 2-way merge 방식을 사용했지만, 추가적인 테이프가 있다면, 이를 확장해 한 번에 여러 개의 런을 병합하는 k-way merge를 수행할 수 있습니다. 이렇게 하면 정렬을 완료하는 데 필요한 병합 패스 수를 줄일 수 있다는 장점이 있습니다.
k개의 런을 병합할 때의 기본 방식식은 기존 2-way merge와 유사합니다. 각 테이프에서 런의 시작 위치로 이동해 첫 번째 원소를 확인하고, 그 중 가장 작은 값을 찾아 출력 테이프에 기록합니다. 이후 해당 런이 위치한 테이프를 한 칸 이동시켜 다음 값을 가져오고, 다시 가장 작은 값을 선택하는 과정을 반복합니다. 이때 런의 수가 많아질수록 최소값을 효율적으로 찾는 것이 중요해지는데, 이를 위해 우선순위 큐 (priority queue)를 사용할 수 있습니다.
- 모든 런에서 첫 값을 priority queue에 넣고,
- 최솟값을 deleteMin 연산으로 꺼낸 뒤 출력 테이프에 기록합니다.
- 이후 그 값을 가져온 테이프에서 다음 값을 queue에 다시 삽입하며
- 런이 끝날 때까지 이 과정을 반복합니다.
예를 들어, 총 3개의 테이프에 다음과 같이 정렬된 런이 있다고 해봅시다.

이들을 한 번에 병합하여 정렬된 데이터를 얻기 위해 3-way merge를 두 번 수행하면 됩니다.


이처럼 k-way 병합을 사용하면, 매 패스마다 각 런의 길이가 k배로 증가하므로, 전체 패스 수는 logₖ(N/M) 로 줄어들게 됩니다.
예를 들어 N = 13, M = 3이라면, log₃(13/3) = 2가 되고,
더 큰 예시로 N = 320, k = 5라면 log₅(320) = 4 패스면 충분합니다.
결과적으로, 추가 테이프를 활용해 k-way merge를 수행하면 전체 정렬 시간을 크게 줄일 수 있고, priority queue를 통해 병합 성능도 효율적으로 유지할 수 있습니다. 이는 외부 정렬에서 매우 중요한 최적화 전략입니다.
Polyphase Merge
앞서 설명한 k-way merge 전략은 일반적으로 2k개의 테이프를 사용해야 한다는 점에서 실용적이지는 않습니다. 그렇기에 사용하는 방식이 Polyphase Merge입니다. 이 병합은 k+1개의 테이프 만으로 k-way 병합을 수행할 수 있게 합니다.
예를 들어, 2-way merge를 3개의 테이프로 수행한다고 하면, T1에 원래 데이터가 있고, 이를 정렬하면 34개의 런이 만들어진다고 가정해봅시다. 단순하게 T2와 T3에 각각 17개의 런을 복사한 다음 병합하면, T1에 17개의 병합된 런이 생깁니다. 문제는, 모든 런이 T1에 존재하기 때문에 다시 병합하려면 또 분산시켜야 한다는 점입니다. 이렇게 되면 매 병합 단계마다 추가적인 반 회차가 필요하게 됩니다.
이를 개선하는 방식이 Polyphase Merge입니다. 여기서는 런의 분포를 불균형하게 나눕니다. 예를 들어, T2에는 21개의 런을, T3에는 13개의 런을 저장합니다. 이 상태에서 T3가 먼저 비워질 때까지, 병합하여 T1에 13개의 병합된 런을 만듭니다. 이후 T1(13개 런)과 T2(8개 런)를 병합해 T3에 쓰고, 다시 T1과 T3를 병합해 T2로 보내는 과정을 반복합니다. 런의 분포 상황은 다음과 같은 테이블로 나타낼 수 있습니다.

이와 같이 폴리페이즈 병합에선 테이프를 번갈아가며 병합 대상 및 출력 대상으로 활용합니다. 런의 초깃값 분포를 어떻게 하느냐에 따라 전체 병합 효율이 좌우됩니다.
추가적으로, 만약 런의 개수가 피보나치 수라면 가장 효율적인 분할이 가능합니다. 예컨데, 34개의 런을 21과 13으로 나누는 것은 피보나치 수 분할이며, 매우 이상적인 형태입니다. 반대로 런의 개수가 피보나치 수가 아니라면, 더 효율적인 병합을 위해 더미 런(dummy run)을 추가해서 런의 수를 피보나치 수로 맞추는 것이 권장됩니다.
Replacement Selection
기본적인 외부 정렬에서는, 메모리에 가능한 한 많은 레코드를 올린 후 이를 정렬해서 출력 테이프에 기록하고, 이 과정을 반복해 여러 개의 "런(run)"을 생성합니다. 하지만 이 방식은 각 런의 길이가 내부 메모리 크기(M)에 제한되기 때문에 런의 수가 많아지고, 결국 병합 횟수도 늘어납니다.
Replacement Selection은 아래 처럼 동작합니다.
- 초기 설정
내부 메모리에 M개의 레코드를 불러와서 최소 힙(또는 priority queue)을 구성합니다. - 런 생성(Run Building)
deleteMin 연산을 통해 힙에서 가장 작은 값을 꺼내 출력 테이프에 기록합니다.
입력 테이프에서 새로운 레코드를 하나 읽어옵니다. (직전 출력 값보다 크거나 같으면, 현재 런에 포함 가능하므로, 힙에 삽입한다. 작으면, 힙이 아니라 dead space에 보관하고, 다음 런을 위해 사용) - 런 종료 및 새 런 시작
힙에 남은 원소가 모두 빠져나가면 하나의 런이 완성됩니다.
이제 dead space에 보관했던 원소들로 새로운 힙을 만들어 다음 런을 시작합니다.
이 과정을 반복합니다. - 효율성
이 기법을 사용하면 평균적으로 각 런의 길이를 2M 정도까지 늘릴 수 있습니다.
예를들어, 기존 방식으로 320개의 런이 생성되던 입력 데이터도, replacement selection을 사용하면 약 160개 런만으로 처리할 수 있게 됩니다.
merge 과정이 적어지기 때문에 전체 외부 정렬에서 디스크 접근 횟수(I/O)가 줄어드는 효과가 큽니다.
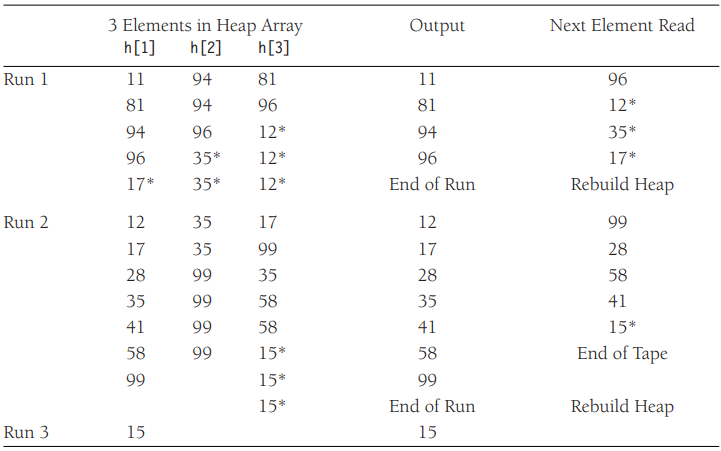
여기서 *(Asterisk)는 dead space에 있는 원소를 의미합니다.
다음 런에서는 [12, 35, 17]로 새 힙을 구성하여 반복합니다.
'( * )Engineering > 🌜C/C++' 카테고리의 다른 글
| Algorithm : Graph Algorithm (1) (0) | 2025.05.09 |
|---|---|
| Algorithm : Sorting (4) (0) | 2025.05.05 |
| Algorithm : Sorting(2) (2) | 2025.05.04 |
| Algorithm : Sorting(1) (0) | 2025.04.28 |
| Algorithm : Algorithm Analysis (0) | 2025.04.27 |

