https://product.kyobobook.co.kr/detail/S000007672724
Data Structures and Algorithm Analysis in C++ | Weiss - 교보문고
Data Structures and Algorithm Analysis in C++ | Advanced Data Structures/Algorithms C++ Data Structures and Algorithm Analysis in C++, 3/e Mark Allen Weiss, Florida International University ISBN : 0-321-37531-9 Mark Allen Weiss teaches readers to reduce ti
product.kyobobook.co.kr
알고리즘 공부 교재.
알고리즘을 공부하면서, "이건 빠르다.", "느리다" 같은 말을 자주 듣습니다. 그런데 그 "빠르다"는 정확히 무슨 뜻일까요? 프로그램을 돌려보면 0.01초가 걸리는 것도 있고, 3초가 걸리는 것도 있습니다. 그런데 어떤 건 데이터가 많아지면 0.01초가 1000초가 되기도 합니다. 이럴 때 필요한 게 바로 Time Complexity(시간 복잡도)입니다.
이번 글에서는 Data Structor and Algorithm Analysis in C++ 2장 내용을 바탕으로 알고리즘의 실행 시간 분석이란 어떤 것이고, 그 분석을 위해 어떤 수학적 도구들이 사용되는지 정리해 보겠습니다.
What is Algorithm?
An algorithm is a clearly specified set of simple instructions to be followed to solve a problem.
알고리즘은 문제를 해결하기 위해 따라야 할 명확하게 지정된 간단한 명령 집합입니다.
문제에 대한 알고리즘이 (어떻게든) 주어지고 옳다고 결정되면, 중요한 단계는 알고리즘이 시간이나 공간과 같은 자원에 얼마나 많은 것을 필요로 하는지 결정하는 것입니다.
문제를 해결하지만 1년이 걸리는 알고리즘은 거의 쓸모가 없고, 마찬가지로 수 천 기가바이트의 메인 메모리가 필요한 알고리즘은(현재) 대부분의 시스템에서 유용하지 않습니다.
Why? : 알고리즘 분석이 필요한 이유
알고리즘은 문제를 "풀기만 하면" 되는 게 아닙니다. 얼마나 빠르고 적은 자원으로 푸는지가 더 중요합니다. 같은 문제라도 1초에 푸는 알고리즘과 1시간 걸리는 알고리즘은 실용성에서 엄청난 차이가 있습니다. 그렇기 때문에 알고리즘 분석은 단순한 프로그래밍이 아니라 컴퓨터 과학의 기초가 되는 개념입니다.
Mathmetical Background
| Notation | Meaning |
| Big-O | Worst Case(Upper Bound) |
| Big-Ω | Best Case(=Lower Bound) |
| Big-Θ | Tight Bound |
| Little-o | Stric Upper Bound |
Big-O : 알고리즘의 최악의 수행 시간을 상한선으로 나타낸 표기법.
Big-Omega : 알고리즘이 최소 이 정도 시간은 걸린다고 보장하는 표기법
Big-Theta : 정확한 차수(상한 = 하한, 둘 다 만족). 알고리즘의 수행 시간을 정확하게 표현할 수 있는 경우.
Little-o : 절대 상한선보다 작다는 것을 의미.

- 두 연산을 순차적으로 수행할 때, 전체 복잡도는 두 복잡도를 더한 것보다 크지 않다.

- 두 연산을 중첩해서 수행할 때, 복잡도는 각 복잡도의 곱이다.

- 로그에 어떤 상수 제곱을 붙여도 로그함수는 선형보다 느리게 성장한다.

+) 추가 내용
1. 극한을 비교.


0분의 0 꼴 이거나, 무한대 분의 무한대 꼴일 때, 로피탈 사용 가능합니다. 로피탈은 미분해서 극한을 비교하는 방식입니다.
하지만 너무 과합니다. 대부분의 경우에는 직관적이고, 단순한 계산으로 충분히 비교할 수 있습니다.
네 번째의 극한이 존재하지 않을 때는 언제일까?

교재에는 이런 문제가 있습니다.
이런 경우에는 둘의 성장 속도를 비교할 수 없는 경우를 만들어야 합니다.

이렇게 정의된 두 함수를 비교한다면 입력 N에 따라 번갈아가며 커지거나 작아지게 됩니다.
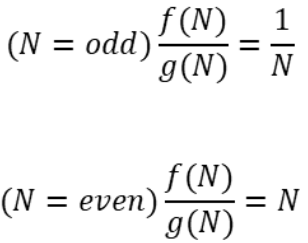
때에 따라 상대적으로 더 크거나 작아지기 때문에 어느 쪽도 작거나 클 수 없습니다.

Model
알고리즘을 분석하기 위해서는 계산 모델이 필요합니다. 이상적인 컴퓨팅 환경을 두고 이론의 본질을 보기 위해서 교재에서는 이와 같은 방법을 사용합니다.
- 이 모델은 덧셈, 곱셈, 비교, 대입 같은 단순한 연산이 각각 정확히 1 단위 시간이 걸린다고 가정합니다.
- 행렬 역행이나 정렬처럼 복잡한 연산은 제외되며, 이는 한 단위 시간 안에 수행될 수 없기 때문입니다.
- 현대 컴퓨터처럼 고정된 크기 정수(ex: 32-bit)를 사용합니다.
- 무한한 메모리를 가정하여, 메모리 용량 제한으로 인한 분석 복잡성을 제거합니다.
What to Analyze
1. Time, 분석의 대상은 실제 시간이 아니다.
컴퓨터 성능, 컴파일러, 운영체제, 하드디스크 속도 등에 따라 실제 실행 시간은 달라집니다. 그렇기 때문에 그런 요소를 고려하지 않고, 알고리즘의 구조 자체가 어떤 성능을 가지는 지에 집중을 합니다.
2. What, 그래서 뭘 분석하는가
입력 크기 N이 커질수록 연산 횟수가 어떻게 증가하는지, 관심 있는 건 Average Case와 Worst Case입니다.
3.Why, 왜 Worst Case를 기준으로 분석하는가?
모든 입력에 대해 보장된 성능을 알고 싶기 때문입니다. 평균 케이스는 입력의 분포를 알아야 하는데, 실제로는 알기 어렵기 때문에 Worst Case를 기준으로 분석하는 경우가 많습니다.

교재에서 다루는 예제입니다.
주어진 정수 배열 A₁, A₂, ..., Aₙ 에 대해 연속된 부분 배열(subarray) 중 합이 최대가 되는 구간의 합을 구하라.
단, 모든 수가 음수일 경우 결과는 0으로 한다.

해당 문제에 대해 책에서는 4가지 알고리즘을 비교하여 보여줍니다. 이를 통해 알 수 있는 건
- 작은 양의 input에서는 4개의 알고리즘이 모두 순식간에 실행되며 속도차이가 크게 나지 않는다.
- Cubic이나 Quadratic로 짜인 알고리즘은 입력 N이 커지면 현실적으로 사용하기 어렵다.


Cubic은 작은 입력 값부터 비교적 가파르게 성장한다. 오른쪽을 보면 확실히 큰 입력에 대해서는 Cubic, Quadratic 모두 사용하지 않는 편이 좋다.
Running-Time Calculations
- for loops
for loop의 실행 시간은 루프 안의 문장 실행 시간 * 반복 횟수로 계산합니다. - nested loops
중첩된 반복문이 있을 경우 안쪽에서 바깥쪽 방향으로 분석합니다.
중첩된 루프 안의 문장에 대한 총 실행 시간은
해당 문장의 실행 시간 * 각 루프의 반복 횟수를 모두 곱한 값입니다. - consecutive statements
여러 문장이 연속해서 나올 경우, 전체 실행 시간은 각각의 실행 시간을 더한 것과 같으며, 결국 가장 큰 시간 복잡도를 가진 쪽이 전체 복잡도를 결정합니다. - if / else
조건문이 있을 경우 전체 실행 시간은 조건 테스트 시간 + S1과 S2 중 더 큰 쪽의 시간입니다
일부 경우 과대평가가 될 수 있지만,
if(condition)
S1;
else
S2;
Maximum Subsequence Sum
Algorithm 1: Brute Force (O(N³))
모든 부분 배열을 다 탐색하면서 합을 구합니다.
3중 루프를 사용하여 구간마다 합을 새로 계산하는 방식입니다.
int MaxSubSum1(const vector<int> &A) {
int maxSum = 0;
int N = A.size();
for (int i = 0; i < N; ++i)
for (int j = i; j < N; ++j) {
int thisSum = 0;
for (int k = i; k <= j; ++k)
thisSum += A[k];
if (thisSum > maxSum)
maxSum = thisSum;
}
return maxSum;
}3중 루프 완전 탐색 코드이기 때문에 시간 복잡도가 매우 높습니다.
Algorithm 2: Improved Enumeration (O(N²))
부분합을 매번 새로 계산하는 대신, 이전 계산 결과를 누적해서 재활용한다. 2중 루프만 사용합니다.
int MaxSubSum2(const vector<int> &A) {
int maxSum = 0;
int N = A.size();
for (int i = 0; i < N; ++i) {
int thisSum = 0;
for (int j = i; j < N; ++j) {
thisSum += A[j];
if (thisSum > maxSum)
maxSum = thisSum;
}
}
return maxSum;
}누적합을 재활용하지만 여전히 큰 시간 복잡도를 갖습니다.
Algorithm 3: Divide and Conquer (O(N log N))
문제를 절반으로 분할해 재귀적으로 해결한다.
최대 부분합은 왼쪽, 오른쪽. 경계를 걸치는 경우 중 하나에 존재하기 때문입니다.
int MaxSubSum3(const vector<int> &A, int left, int right) {
if (left == right) // Base case
return max(0, A[left]);
int center = (left + right) / 2;
int maxLeftSum = MaxSubSum3(A, left, center);
int maxRightSum = MaxSubSum3(A, center + 1, right);
int maxLeftBorderSum = 0, leftBorderSum = 0;
for (int i = center; i >= left; --i) {
leftBorderSum += A[i];
if (leftBorderSum > maxLeftBorderSum)
maxLeftBorderSum = leftBorderSum;
}
int maxRightBorderSum = 0, rightBorderSum = 0;
for (int j = center + 1; j <= right; ++j) {
rightBorderSum += A[j];
if (rightBorderSum > maxRightBorderSum)
maxRightBorderSum = rightBorderSum;
}
return max({ maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum });
}0이 될 때까지 반으로 나누고 더 하면서 확인하는 방법.
사용 시 :
MaxSubSum3(A, 0, A.size() - 1);처럼 호출해야 합니다.
Algorithm 4: Kadane’s Algorithm (O(N))
배열을 한 번만 스캔하면서 현재 부분합(thisSum)과 전체 최대합(maxSum)을 관리합니다.
연속 부분합이 음수가 되면 0으로 초기화하여 다시 시작하도록 한 알고리즘입니다.
int MaxSubSum4(const vector<int> &A) {
int maxSum = 0, thisSum = 0;
for (int j = 0; j < A.size(); ++j) {
thisSum += A[j];
if (thisSum > maxSum)
maxSum = thisSum;
else if (thisSum < 0)
thisSum = 0;
}
return maxSum;
}'( * )Engineering > 🌜C/C++' 카테고리의 다른 글
| Algorithm : Sorting(2) (2) | 2025.05.04 |
|---|---|
| Algorithm : Sorting(1) (0) | 2025.04.28 |
| C++ : Value Category (0) | 2025.04.27 |
| C++ : Dependent Type / Auto (0) | 2025.04.24 |
| C++ : Templates (0) | 2025.04.13 |

