Algorithm : Sorting(2)

( * )Engineering/🌜C／C++

Algorithm : Sorting(2)

Nekoder

|2025. 5. 4. 23:51

728x90

저번에 이어서 계속 정렬을 다루어보겠습니다. sorting이 볼륨이 꽤 큽니다.

Heapsort

Heapsort is an algorithm that can sort an array in O(N log N) time.

힙 정렬은 배열을 O(N log N)시간 안에 정렬할 수 있는 알고리즘이다.

Heap이라는 자료 구조를 이용합니다. 배열을 힙으로 만들어서, 가장 큰(혹은 가장 작은) 요소를 루트로 올립니다. 그 다음, 루트 요소를 배열 끝으로 보내고, 다시 힙을 정리하는 과정을 반복합니다. 순서대로 보자면

먼저 배열을 힙 형태로 만듭니다.(Heapify)
루트에 있는 최대값을 배열 마지막 위치로 이동합니다.
힙 크기를 하나 줄이고, 다시 힙을 재정렬합니다.
이 과정을 배열이 모두 정렬될 때까지 반복합니다.

힙에서는 맨 위 노드를 루트 노드라고 부르고 항상 가장 크거나 가장 작은 값입니다. 루트로 올린다는 말은 데이터를 재배치해서 가장 큰 값을 트리의 맨위(루트)에 위치시키는 걸 의미합니다. 힙은 완전 이진 트리 구조(Complete Binary Tree) 입니다. 이진 트리 안에서, 부모 노드가 자식 노드보다 항상 크거나 같아야 합니다(Max heap 기준). 그래서 힙을 만들 때, 하는 일은 : 트리 구조를 맞추면서 큰 값을 위로 끌어올리고, 작은 값은 아래로 보내는 방식입니다.

[10, 5, 3, 2, 4]

이 배열을 힙(트리)로 보면

10이 루트입니다. 5, 3은 그 다음 큰 값들, 2, 4 는 가장 작은 값들. 루트로 올렸다는 말은 지금처럼 가장 큰 값 10을 루트에 위치시킨 상태를 만드는 걸 말합니다.

교재에 있는 예제 코드 살펴보겠습니다.

template<typename Comparable>
void heapsort(vector<Comparable>& a){
	for(int i = a.size() / 2 - 1; i >= 0; --i) { /*buildHeap*/
    	percDown(a, i, a.size());
    }
    for(int j = a.size() -1; j > 0; --j){ /*deleteMax*/
    	std::swap(a[0], a[j]);
        percDown(a, 0, j);
    }
}

inline int leftChild(int i){
	return 2 * i + 1;
}

template<typename Comparable>
void percDown(vector<Comparable>& a, int i, int n){
	int child;
    Comparable tmp;
    
    for(tmp = std::move(a[i]); leftChild(i) <n; i = child){
    	child = leftChild(i);
        if(child != n-1 && a[child] < a[child + 1]){
        	++child;
        }
        if(tmp < a[child]){
        	a[i] = std::move(a[child]);
        }
        else {
        	break;
        }
        a[i] = std::move(tmp);
    }
}

흐름을 체크해보겠습니다.

처음에는 절반으로 나눠서 진행합니다. 왜냐하면 트리 구조라서 뒤에는 작은 값만 오기 때문입니다. 그래서 배열의 중간부터 왼쪽(부모들)으로 percDown을 시작합니다.

leftChild 함수 사용해서 현 노드의 왼쪽 자식(i)의 인덱스를 찾습니다. 그 후 오른쪽 자식과 비교하여 큰 쪽을 고르고 값을 부모로 부터 임시로 받은 tmp와 비교해서 자식이 크다면 자식을 부모로 올립니다.(루트로 올린다.) 이걸 절반부터 옆으로 당기면서 계속 반복합니다. 이게 빌드힙 입니다.

그 후에 루트를 배열 끝과 std::swap 한 후에 배열 크기를 1 줄입니다. 그 후 0번 째 요소를 percDown해서 자식들과 비교하면서 큰 값을 부모로 끌어올리고, tmp(기존 루트 값)는 자연스럽게 적절한 자리로 내려가게끔 합니다. 이게 deleteMax입니다.

deleteMax가 이해가 안된다면

[50, 30, 40, 10, 20]

만약 빌드힙이 끝난 상태가 위와 같다고 하겠습니다. 0번 인덱스는 50이고 최대값입니다.

여기서 swap이 일어나면 0번과 4번을 swap합니다.

[20, 30, 40, 10, 50]

50은 확정된 값이니까 맨 끝으로 빠졌습니다.

이제 현재 루트는 20입니다. 20은 자식들과 비교해서 힙 성질을 만족해야 합니다.

leftChild(0) = 1 >> 30

rightChild(0) = 2 >> 40(letf다음 인덱스)

30 < 40 이라서 40을 반환하고, 40 > 20이니까 40을 0번(루트)로 끌어올리고, 20을 2번으로 내려 보냅니다.

[40, 30, 20, 10, 50]

다시 percDown이 일어나고 2번에 있는 20이 다시 자식들과 비교해 하지만, 더 이상 내려갈 곳이 없기 때문에 멈춥니다.

최종적으로 1회 deleteMax가 일어나면

[40, 30, 20, 10] [50]

이렇게 완료됩니다.

Mergesort

이번에 다루는 내용은 mergesort(병합 정렬) 입니다. 병합 정렬은 Divide and Conquer 전략을 사용합니다. 문제를 절반으로 쪼개고, 각각 정렬한 다음 합치는 방식입니다.

흐름 살펴보겠습니다.

배열을 계속 반으로 나눕니다.
더 이상 나눌 수 없을 때까지(크기 1이 될 때까지) 재귀 호출합니다.
두 정렬된 배열을 merge함수로 합칩니다.

2. 다음은 A[Actr] = 13, B[Bctr] = 2 비교한다.
2 < 13 이므로, 2를 C[Cctr]에 복사한다.
Cctr을 오른쪽으로 이동하고, Bctr도 다음 요소(15)로 이동한다.

3. A[Actr] = 13, B[Bctr] = 15 비교한다.
13 < 15 이므로, 13을 C[Cctr]에 복사한다.
Cctr 이동, Actr 이동.

4.A[Actr] = 24, B[Bctr] = 27 비교한다.

24 < 27 이므로, 24를 C[Cctr]에 복사한다.

Cctr 이동, Actr 이동.

A[Actr] = 26, B[Bctr] = 27 비교한다.
26 < 27 이므로, 26을 C[Cctr]에 복사한다.
Cctr 이동, Actr 이동.

이제 배열 A의 요소를 모두 다 복사했다.
남은 배열 B의 [27, 38]은 순서대로 C에 복사한다.

template<typename Comparable>
void mergeSort(vector<Comparable>& a){
    vector<Comparable> tmpArray(a.size());
    mergeSort(a, tmpArray, 0, a.size() - 1);
}

template<typename Comparable>
void mergeSort(vector<Comparable> &a, vector<Comparable> & tmpArray, int left, int right){
    if(left < right){
        int center = (left + right) / 2;
        mergeSort(a, tmpArray, left, center);
        mergeSort(a, tmpArray, center + 1, right);
        merge(a, tmpArray, left, center + 1, right);
    }
}

입력 배열 a, 임시 배열 tmpArray, 구간 [left, right]를 받습니다.

left < right 조건이 성립하면, 배열을 center 기준으로 반으로 나눈다. 왼쪽 구간[left, center]를 재귀적으로 정렬합니다. 오른쪽 구간[center+1, right]를 재귀적으로 정렬합니다. 마지막으로 merge함수를 사용해 정렬된 두 부분을 합칩니다.

이 함수는 단순히 배열을 계속 나누고, 나중에 합치는 일을 위임하는 역할만 하고 있습니다. 정렬 자체는 merge함수가 담당합니다.

template <typename Comparable>
void merge(vector<Comparable> & a, vector<Comparable> & tmpArray, int leftPos, int rightPos, int rightEnd)
{
    int leftEnd = rightPos - 1;
    int tmpPos = leftPos;
    int numElements = rightEnd - leftPos + 1;

    while (leftPos <= leftEnd && rightPos <= rightEnd)
        if (a[leftPos] <= a[rightPos])
            tmpArray[tmpPos++] = std::move(a[leftPos++]);
        else
            tmpArray[tmpPos++] = std::move(a[rightPos++]);

    while (leftPos <= leftEnd)
        tmpArray[tmpPos++] = std::move(a[leftPos++]);

    while (rightPos <= rightEnd)
        tmpArray[tmpPos++] = std::move(a[rightPos++]);

    for (int i = 0; i < numElements; ++i, --rightEnd)
        a[rightEnd] = std::move(tmpArray[rightEnd]);
}

입력 배열 a, 임시 배열 tmpArray, 그리고 병합할 두 구간의 시작/끝 포지션을 받습니다.

leftPos ~ leftEnd는 왼쪽 정렬 구간.

rightPos ~ rightEnd는 오른쪽 정렬구간.

왼쪽 요소와 오른쪽 요소를 비교해서 더 작은 쪽을 tmpArray에 복사합니다.

둘 중 하나가 다 복사되면, 남은 다른 쪽 전체를 tmpArray에 복사합니다.

tmpArray에 있는 결과를 다시 원래 배열 a로 복사합니다.

정렬은 바로 여기서 일어납니다. 비교-이동을 하면서 순서대로 임시 배열에 넣습니다. 따라서 mergesort는 "나누는 것" 보다 "merge"과정이 진짜 핵심입니다.

그렇다면 왜 merge과정이 O(N) 일까?

병합 과정에서는 왼쪽 배열과 오른쪽 배열을 각각 하나의 포인터로 가리킵니다. 포인터를 한 번 움직일 때 마다, 원소 하나를 처리합니다. 그렇기 때문에 비교에서 N-1번, 복사에서 N번의 연산이 발생하기 때문에 결국 O(N) 만큼의 비교와 이동이 발생합니다.

그래서 divide과정에서 O(log N) conquer(merge)에서 O(N)의 작업도를 갖습니다. 따라서 전체 시간 복잡도는 O(N log N)이 되는 걸 확인했습니다.

Quicksort

이번에 다루는 내용은 퀵소트입니다. 퀵소트도 Divide and Conquer 전략을 사용합니다. 하지만 merge sort처럼 "합칠 때 정렬"하는 게 아니라, 나누는 과정(분할) 에서 바로 정렬을 진행한다는 차이가 있습니다.

퀵소트 흐름

배열에서 하나의 pivot(피벗)을 선택합니다.
pivot보다 작은 요소들은 왼쪽, 큰 요소들은 오른쪽으로 분할합니다. (partition 과정)
왼쪽과 오른쪽 부분 배열을 각각 재귀적으로 정렬합니다.

이 과정을 배열이 길이 1 이하가 될 때까지 반복합니다.

피벗은 어떻게 선택할까?

1. Wrong Way (잘못된 방식)

항상 첫 번째 요소를 pivot으로 선택하는 방법을 말합니다.(배열의 가장 왼쪽에 있는 값을 pivot으로 삼아서 분할)

문제점

만약 배열이 이미 정렬된 상태이거나, 거의 정렬된 상태이면, 항상 최악의 분할이 일어납니다.

결과적으로 한쪽 부분 배열은 요소가 1개, 다른 한쪽 부분 배열은 거의 전체를 포함하게 되기에, 이렇게 되면 재귀 깊이가 깊어지고, 전체 정렬 시간이 O(N²) 로 떨어집니다.

2. A Safe Maneuver (안전한 조치)

pivot을 그냥 배열의 중간 요소(a[(left + right) / 2])로 선택하는 방법입니다.

장점

배열이 정렬되어 있어도 중간값을 고르기 때문에, 최소한 완전히 한쪽으로만 쏠리는 최악의 상황은 피할 수 있습니다.

문제점

배열이 매우 비대칭한 분포를 가질 경우(예: 중간이 가장 크거나 작을 경우)에는여전히 좋은 분할이 안 될 수 있습니다.

그냥 중간값을 pivot으로 고르는 것만으로도 첫 번째 값만 고르는 것보단 훨씬 낫지만, 최선은 아닙니다.

3. Median-of-Three Partitioning (삼중 선택법)

pivot을 left, center, right 세 개 요소를 골라서이 중 중간값을 pivot으로 삼는 방법입니다.

구체적인 절차

배열의 가장 왼쪽 요소(a[left]), 중간 요소(a[center]), 오른쪽 요소(a[right])를 선택.
이 셋을 비교해서 median(중간값)을 찾음.
이 median 값을 pivot으로 사용.
이 pivot을 right-1 자리에 옮겨서 partition할 때 빼고 비교.

장점

pivot을 좀 더 균형 잡힌 값으로 선택할 수 있습니다.
정렬된 배열, 역순 배열, 부분 정렬된 배열에 대해 모두 좋은 성능을 낼 수 있습니다.
최악의 경우를 피하면서 평균 성능을 O(N log N) 수준으로 안정적으로 유지할 수 있습니다.

median-of-three는 pivot 선택의 편향을 줄여서 퀵소트의 평균 성능을 높이는 매우 좋은 전략입니다.

추가로 random과, median-of-medians 방식이 있는데, 제일 자주 사용하고 실용성이 높은 방법은 random과 median-of-three라고 합니다. random은 말 그대로 랜덤으로 피벗을 선택하는 방식을 의미합니다.

Partitioning Strategy

partition은 배열울 pivot을 기준으로 나누는 작업입니다.

목표 : pivot 보다 작은 값들은 왼쪽에, pivot보다 큰 값들은 오른쪽에 모으는 것.

partition 구현 핵심 흐름

pivot을 먼저 배열의 적당한 위치(보통 right-1)로 옮겨놓는다.
왼쪽 끝(i)에서 오른쪽으로 가면서 pivot보다 큰 값을 찾는다.
오른쪽 끝(j)에서 왼쪽으로 가면서 pivot보다 작은 값을 찾는다.
i < j일 동안 이 두 값을 swap한다.
포인터가 교차되면(i ≥ j) 루프를 멈춘다.
pivot을 i 위치에 swap해서 복구한다.

Analysis of Quicksort

이 부분은 퀵소트의 시간 복잡도를 최악, 최선, 평균으로 나눠서 분석하고 있습니다.

먼저 퀵소트의 기본 재귀식입니다. 기본적으로는 피벗을 기준으로 두 부분으로 나눈 뒤, 양쪽을 다시 퀵소트하고, 파티션은 선형 시간이 걸립니다.

여기서 i는 피벗보다 작은 원소 개수
cN은 파티션에 드는 선형 시간

Worst Case

매번 피벗이 가장 작은 원소일 때

이 경우 i = 0, 재귀식은 아래처럼 단순화됩니다.

이걸 전개하면

즉 최악의 경우에는 O(N²) 시간 걸립니다. 입력이 정렬되어 있거나 반대로 정렬되어 있을 때 이런 경우가 생깁니다.

Best Case

매번 피벗이 정확히 중앙에 위치할 때

이 경우 하위 배열 두 개가 정확히 절반으로 나뉘기에

이것도 전개해보면,

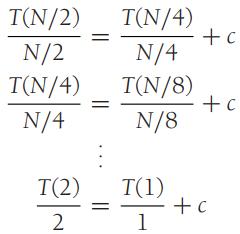
즉 최선에 경우에는 O(N log N) 시간 복잡도를 갖습니다.

Average Case

피벗이 어떤 위치에 올 확률이 모두 동일하다고 가정해봅시다. 그렇다면 평균적으로 아래의 재귀식을 얻게 됩니다.

이 식을 재귀식으로 전개해서 정리하면

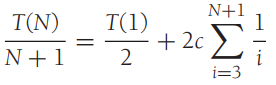
따라서 평균적인 경우에도 mergesort와 동일한 시간 복잡도를 갖습니다. 하지만 실제 실행 속도는 파티션이 제자리에서 일어나기 때문에 퀵소트가 더 빠릅니다.

A Linear-Expected-Time Algorithm for Selection

퀵소트를 변형하여 k번째로 작은 원소를 찾는 Quickselect 알고리즘을 다룹니다.

Quickselect는 아래와 같이 동작합니다.

입력이 1개일 경우, 그 원소를 그대로 반환 (기저 조건).
pivot을 하나 선택한다.
pivot을 기준으로 작거나 같은 S1, 큰 S2로 나눈다.
k ≤ |S1|이면 S1에서 다시 탐색
k == |S1| + 1이면 pivot이 정답
k > |S1| + 1이면 S2에서 k - |S1| - 1번째 원소를 찾는다

퀵소트와의 차이점은 재귀 호출이 한 번만 발생한다는 점입니다. 퀵소트는 두 번 호출합니다.

시간 복잡도 분석

Worst case: O(N²) partition이 항상 한쪽으로만 쏠리는 경우

Average case: O(N) 균등하게 잘 나뉘는 경우

정렬 기반 선택과의 비교

priority queue를 이용하면 O(N + k log N)

배열 정렬 후 선택하면 O(N log N)

하지만 퀵셀렉트는 평균적으로 O(N)이며, 특히 중간값을 찾을 때 효율적입니다.

사용자 진입 함수 : 외부에서 k번째로 작은 원소를 찾기 위해 호출.

k는 1부터 시작하는 인덱스임에 유의해야 함(0-based 아님)

template <typename Comparable>
const Comparable & quickSelect(vector<Comparable> & a, int left, int right, int k)
{
    if (left + 10 <= right)
    {
        Comparable pivot = median3(a, left, right);  // 중앙값 피벗 선택 (median-of-three)

        // 피벗을 기준으로 파티션 진행
        int i = left, j = right - 1;
        for (;;)
        {
            while (a[++i] < pivot) {}     // 왼쪽부터 pivot보다 큰 원소 찾기
            while (pivot < a[--j]) {}     // 오른쪽부터 pivot보다 작은 원소 찾기
            if (i < j)
                std::swap(a[i], a[j]);    // 두 원소 교환
            else
                break;                    // 인덱스가 교차하면 루프 종료
        }

        std::swap(a[i], a[right - 1]);    // 피벗을 제자리(i 위치)로 이동

        // 재귀 조건: 피벗 기준으로 k의 위치를 판별
        if (k <= i)
            return quickSelect(a, left, i - 1, k);       // 왼쪽 부분에서 탐색
        else if (k > i + 1)
            return quickSelect(a, i + 1, right, k);      // 오른쪽 부분에서 탐색
        else
            return a[i];                                 // i 위치가 k번째라면 결과 반환
    }
    else
    {
        // 요소 수가 적을 경우 삽입 정렬로 처리
        insertionSort(a, left, right);
        return a[k];
    }
}

median: pivot을 고를 때 3개 중 중간값을 선택해 최악의 경우를 줄임.

partition : 퀵소트와 동일하게 좌우를 나눔.

재귀 호출은 한 번만 일어남 O(N) 기대 성능

작은 크기 이면 insertionSort로 전환해서 성능 최적화

728x90

'( * )Engineering > 🌜C／C++' 카테고리의 다른 글

Algorithm : Sorting (4) (0)	2025.05.05
Algorithm : Sorting (3) (2)	2025.05.04
Algorithm : Sorting(1) (0)	2025.04.28
Algorithm : Algorithm Analysis (0)	2025.04.27
C++ : Value Category (0)	2025.04.27